将军饮马进阶探讨:三线型的将军饮马问题
- 教育
- 1周前
- 533
三线型将军饮马问题

打开百度APP看高清图片
如图,点P为△ABC内一点,M、N、O分别为AB、BC、AC上的动点。问:当M、N、O在何处时可使四边形MNOP周长最小?
分析问题这个问题有解吗?如果有,那该怎么做?
要解决这个较复杂的将军饮马问题,不妨先回顾一下简单的将军饮马问题。
1、先来看最简单的“两点一线”
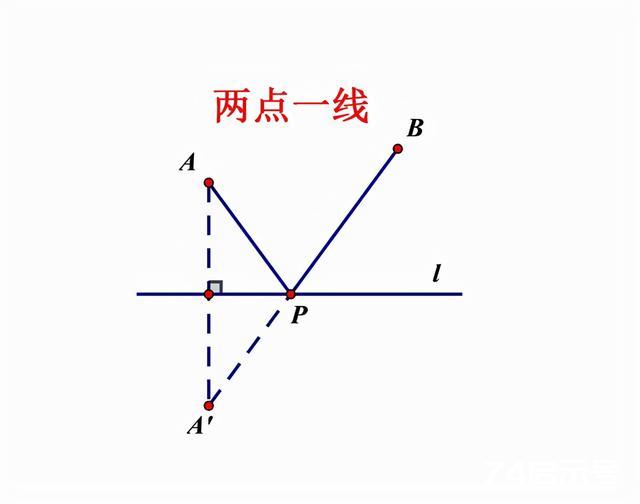
先作其中一点的对称点,然后连接对称点和另一点,连线与直线的交点即为所求。
2、两线一点
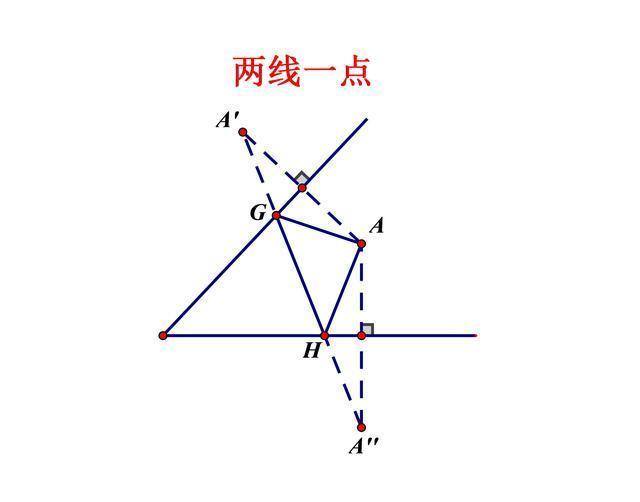
一线变两线,由原来的对称一次变为对称两次。
3、两线两点

两线对称两次,靠哪边哪边为对称轴。
以上为将军饮马问题的三个基本类型,可以看出:无论是一线型还是两线型,最终都要归结为两点间的距离问题,基本依据都是两点之间线段最短。由此,我们确定三线型的基本思路:基本依据不变,化曲为直,把4条线段转化为一条线段,图形基本变换仍然是优先考虑轴对称。
解决问题不妨先仿“两线一点”试着画一下

P'P''显然不是最短路径,因为必须通过AB、BC、AC三条线,然而任何一条线段都不可能同时与这三条线相交!难道无解了吗?别忘了转化思想和对称变换,只要把AC沿BC对称问题就可以迎刃而解。

最后再把图形和步骤整理完善一下

步骤:
(1)分别作点P关于AB、BC的对称点P'和P''
(2)作AC关于BC的对称线段A'C
(3)作点P''关于A'C的对称点P'''
(4)连接P'P''',分别交AB、BC、A'C于点M、N、O'
(5)过点O作OO'⊥BC,交AC于点O(相当于作点O'关于BC的对称点O)
(6)连接PM、MN、NO、OP,四边形MNOP即为所求
小结将军饮马问题即利用轴对称变换把折线路径转化为两点间距离,化曲为直,依据两点之间线段最短求得最短路径,可利用两边之和大于第三边作简单证明。
三个步骤:①作对称;②定交点;③连路径。
补充三线两点

三线三点

三线三点实质是2个两线两点模型的组合








