已知2BC=CD,求∠D
- 教育
- 5天前
- 387
已知2BC=CD,求∠D。你会做吗?
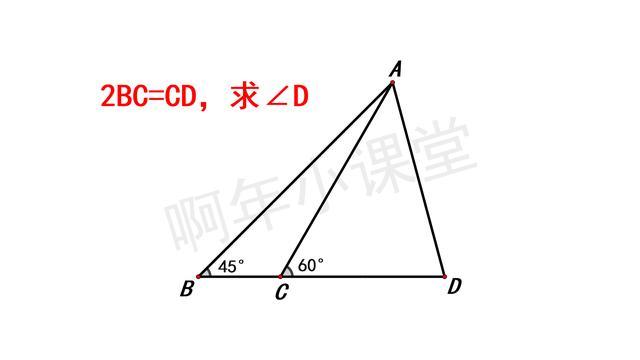
从图中可以看到,∠ABC=45°,∠ACD=60°,45°和60°是特殊角,在直角三角形中非常有用,我们是不是要去构造直角三角形呢?如何构造?
比较容易想到的是过点A作BD的垂线。
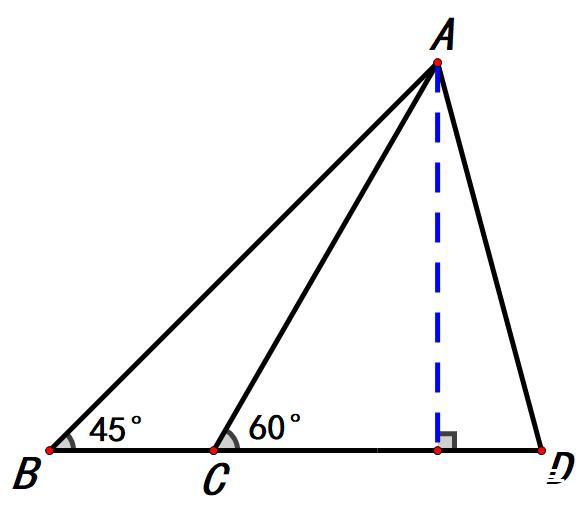
但是作出这条辅助线,并没有给我们太多的有效信息。
除此之外,我们还可以过点D作AC的垂线。
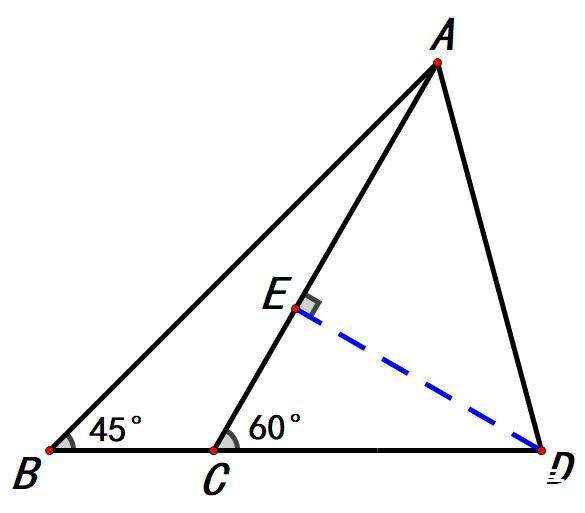
如图,DE⊥AC。
∠BDE=30°,三角形CDE为30°、60°直角三角形,2CE=CD。
而2BC=CD,由此可得CE=BC。

接下来我们连接BE,就能得到一个等腰三角形BCE,∠BEC=∠EBC。
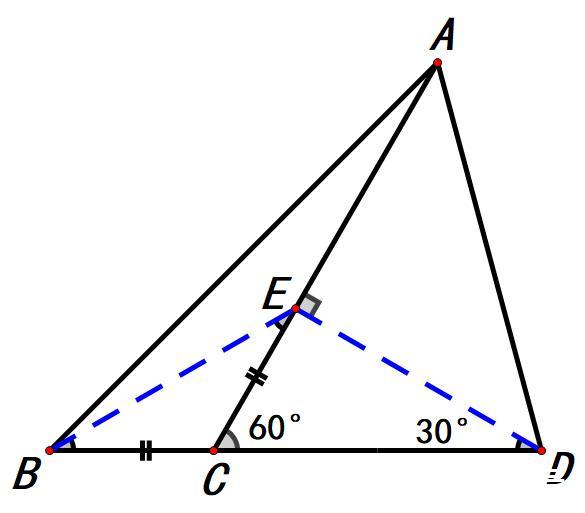
根据三角形的外角定理(三角形的一个外角等于与它不相邻的两个内角之和),
∠BEC+∠EBC=∠ACD=60°,∠ABC+∠BAC=∠ACD=60°,
所以∠BEC=∠EBC=30°,∠BAC=∠ACD-∠ABC=60°-45°=15°,
∠ABE=∠ABC-∠EBC=45°-30°=15°。

∠EBD=∠BDE=30°,∠BAE=∠ABE=15°,
三角形BED和三角形ABE都是等腰三角形,
BE=DE,BE=AE,
等量代换可得DE=AE,
也就是说三角形ADE为等腰直角三角形,∠ADE=45°,
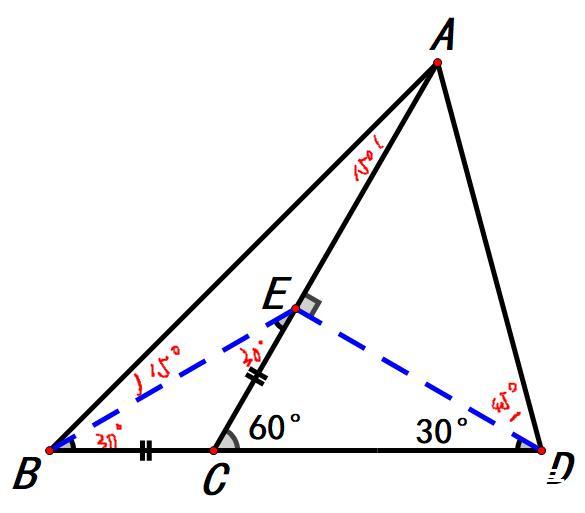
∠D=∠ADE+∠BDE=45°+30°=75°。
你可能想看:
下一篇
立兼向








